Modelo de decaimiento radiactivo
Sustituya monedas por radiación.
También un modelo de la vida media de virus en superficies
Sustituya monedas por virus.
(Esta es la traducción de un "bocadillo científico" del Exploratorium de San Francisco, bajo la alianza con CIENTEC. Puede encontrarlo en inglés aquí.)

Lance cien monedas, separe todas las que queden en posición de “cruz”, coloque unas sobre otras, repita el proceso. De esta manera, usted genera su propio modelo práctico para representar el fenómeno de la desintegración radiactiva o decaimiento exponencial. Los grupos de monedas apiladas muestran gráficamente el significado del término "vida media".
Nota de aprendizaje respecto a COVID-19:
La vida media es también la forma en que los científicos describen cuánto tiempo puede permanecer el coronavirus en diferentes superficies. Como el virus no puede reproducirse fuera del cuerpo, éste se inactivará lentamente con el tiempo, con una duración variable, que dependerá de la superficie en la que se encuentre. Los científicos descubrieron recientemente que la vida media del nuevo coronavirus en cartón es de aproximadamente cuatro horas. Eso significa que alrededor de la mitad de los virus presentes se inactivan después de cuatro horas, y la otra mitad, cuatro horas después de eso. Después de 24 horas, más del 98% del virus debería estar inactivo.
|
Temas: |
Palabras clave: |
Materiales y herramientas
- Al menos 100 monedas.
- Un recipiente para guardar las monedas.
- Opcional: 100 cubos de madera pequeños de aproximadamente 2/5 pulgadas (1 cm) de lado, con una cara del cubo pintada de rojo.

Montaje del experimento
No se requiere.
________________________________________
Descripción de la actividad
Lance todas las monedas sobre la superficie de la mesa. Note que algunas caen en posición de “cara” hacia arriba, o bien, “cruz”. Retire aquellas que se encuentran en posición de “cruz” hacia arriba y colóquelas al lado izquierdo de la mesa, dispuestas en una columna alta.
Recolecte las monedas restantes y realice el lanzamiento de nuevo. Separe las monedas que quedan en posición de “cruz” y colóquelas en una segunda columna, justo al lado de la primera. Repita este experimento hasta que se hayan eliminado todas las monedas. En caso de que no obtenga monedas en posición de “cruz” en un lanzamiento, deje una columna vacía.
Puede realizar esta misma actividad con los cubos de madera, si los tiene, quitando los cubos que aterrizan con el lado rojo hacia arriba.
________________________________________
¿Qué está sucediendo?
La probabilidad de que una moneda aterrice en posición de “cruz” en cualquier lanzamiento es siempre la misma; es el 50%. Así, después del primer lanzamiento, se retiran las monedas que caen en “cruz” y quedan como la mitad de las monedas en el suelo.
En el segundo lanzamiento, nuevamente se obtiene la mitad de las monedas en posición de “cruz”; no obstante, hay menos monedas para comenzar. Después del primer lanzamiento, quedan aproximadamente 1/2 de la mitad de las monedas originales; después del segundo, aproximadamente 1/4; luego 1/8, 1/16, y así sucesivamente. Estos números pueden escribirse en términos de potencias, o exponentes, de 1/2: 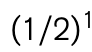 ,
, 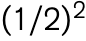 ,
, 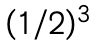 y
y 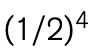 . Este tipo de patrón, en el que una cantidad disminuye repetidamente en una fracción fija (en este caso, 1/2), se conoce como decaimiento exponencial.
. Este tipo de patrón, en el que una cantidad disminuye repetidamente en una fracción fija (en este caso, 1/2), se conoce como decaimiento exponencial.

Cada vez que usted lanza las monedas restantes, se elimina aproximadamente la mitad. El tiempo que tarda en remover la mitad de las monedas restantes, se denomina “vida media”. Para este modelo experimental, en específico, la vida media de las monedas es de un lanzamiento.
Si utiliza cubos de madera pintados, la probabilidad de que un cubo caiga con el lado rojo hacia arriba es 1/6. (Cada cubo tiene seis lados, y solo uno de esos lados está pintado de rojo.) Se necesitan tres lanzamientos para que eliminar aproximadamente la mitad de los cubos, por lo que la vida media de los cubos es de aproximadamente tres lanzamientos. Después de un lanzamiento, quedan 5/6; después de dos lanzamientos, quedan 5/6 de 5/6, o 25/36; y después de tres lanzamientos, 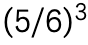 = 125/216 de los cubos.
= 125/216 de los cubos.
El lanzamiento de las monedas o cubos es un proceso impredecible y aleatorio. Rara vez se observará una reducción exacta de 1/2 de las monedas o 1/6 de los cubos en el primer intento. Sin embargo, si repite el primer lanzamiento muchas, muchas veces, el número promedio de monedas que se reducen se acercará a 1/2 (o los cubos eliminados se acercarán a 1/6).
En este modelo, la eliminación de una moneda o un cubo corresponde al decaimiento de un núcleo radiactivo. La probabilidad de que un núcleo radiactivo particular, en una muestra de núcleos idénticos, se descomponga en cada segundo es la misma para cada segundo que pasa, al igual que la probabilidad de que una moneda aterrice en posición de “cruz” es la misma para cada lanzamiento (1/2) o que la probabilidad de que un cubo caiga con el lado rojo hacia arriba es la misma (1/6).
Cuanto menor sea la posibilidad de decaimiento, mayor será la vida media (tiempo para que se descomponga la mitad de la muestra) del isótopo radiactivo particular. Los cubos, por ejemplo, poseen una vida media más larga que las monedas. Para el uranio 238, la posibilidad de decaimiento es pequeña: su vida media es de 4.5 billones de años. Para el radón 217, en cambio, la posibilidad de descomposición es grande: su vida media es una milésima de segundo.
________________________________________
Investigación adicional
Algunos núcleos radiactivos, llamados madres, decaen hacia otros núcleos radiactivos, llamados hijas. Para simular este proceso, comience con 100 monedas de mayor denominación que las pequeñas. Revuélvalas y reemplace las monedas de mayor denominación que aterrizan en posición de “cruz” hacia arriba por las monedas pequeñas. Realice un nuevo lanzamiento con las monedas mezcladas. Haga una columna con todas las monedas que caen en posición de “cruz” y reemplace aquellas monedas de mayor denominación por las monedas pequeñas. Las monedas de mayor denominación representan los núcleos madre; las originales, los núcleos hijas. Observe que las columnas de monedas en decaimiento crecen de manera inicial, y posteriormente se descomponen.
(Traducción autorizada por la fuente por Carla Gómez-Quirós y Alejandra León-Castellá, CIENTEC)
"Attribution: Exploratorium Teacher Institute"
Enlaces relacionados
Decrecimiento exponencial- Matex1minuto
