Matemática y eclipses

Escuche el podcast: Matemática y eclipses

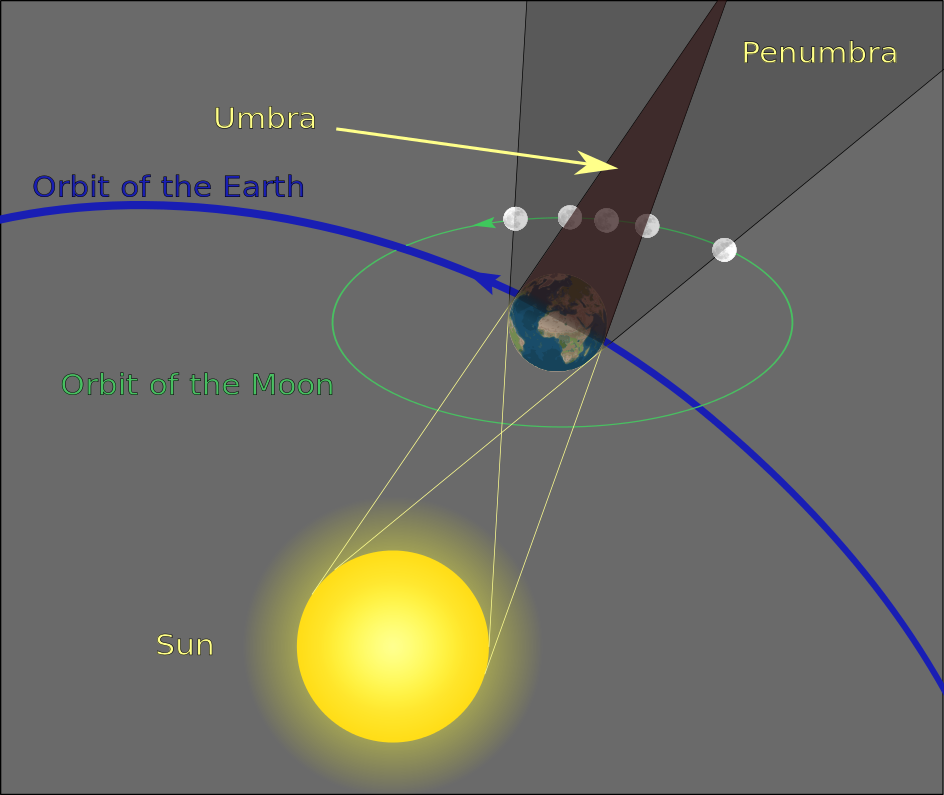
Cada año se pueden contar entre 0 y 3 eclipses Lunares en la Tierra. Estos pueden ser totales, cuando la Luna cruza la umbra, el cono de sombra oscura de la Tierra.  Pero también puede ser parciales, cuando la Luna pasa más tangencial a este cono de sombra.

Desde la perspectiva geométrica, los eclipses son muy interesesantes.  Son un juego de esferas en movimiento, cuyos conos de sombra se cruzan.

Resulta que la alineación del Sol,  la Luna y la Tierra es muy poco frecuente. Eso solo se daría si los centros de los tres astros se cruzan con un mismo eje.  Pero la sombra de la Tierra es grande y esto facilita que aunque no estén totalmente alineados, la Luna se sumerja en ella y se eclipse.

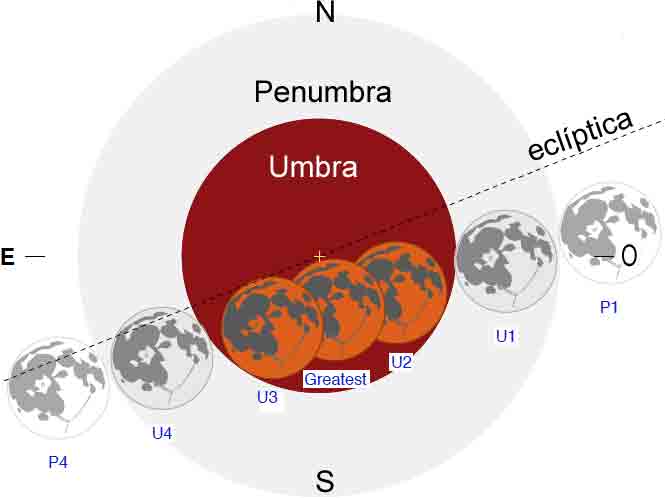
Es tan grande la sombra cruzada por la Luna, que su diámetro casi acomoda tres lunas en fila, una junto a la otra.  ¡Imagíneselo! De ahí que la fase total de un eclipse pueda durar más de 100 minutos.

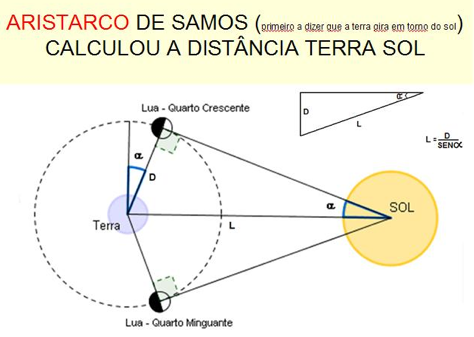
La historia cuenta que un eclipse lunar y la trigonometría, fueron los elementos usados por Aristarco de Samos en el siglo III AC para calcular la distancia entre la Tierra y la Luna. Un hecho sobresaliente para el intelecto humano.

Esta es una producción de Radio Universidad de Costa Rica, CIENTEC, UNA, UNED y TEC con el respaldo del Fondo Especial para el Financiamiento de la Educación Superior Estatal, FEES.

Guión: Alejandra León Castellá, CIENTEC

Edición: Alberto Soto, UNED

Edición radial: Stefany Díaz y Leonardo León.

Locución: Mariana Rivera

Coordinación y publicación: Alejandra León Castellá

Visite también los programas iniciales de Matex1minuto en el blog

Referencias:

Como midió Aristarco la Luna y el Sol. Juan Meléndez Sánchez, Universidad Carlos III de Madrid