| --> índice de matemática |
|
Actividad 1:
Patrones fractales geométricos Curva de Koch (curva de Copo de nieve) Uno de los más sencillos y más elegantes que conozco. |
|
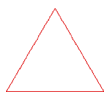 |
Paso 1: Un triángulo equilátero inscrito en un círculo (no mostrado) es la primera iteración de este patrón. El largo de cada lado es 1, el perímetro = 3. |
 |
Paso 2: Divida cada lado del triángulo en 3 partes iguales y dibuje otro triángulo equilátero en el segmento central.
Así resulta una estrella de seis esquinas como segunda iteración. Su perímetro = 3 x 4/3 |
 |
Paso 3: En la tercera iteración del patrón, P = 3 x 4/3 x 4/3. |
 |
Teóricamente usted puede repetir los pasos, dibujando triángulos equiláteros infinitamente.
Siga calculando el perímetro. Lo interesante es notar que el perímetro sigue creciendo, conforme el copo crece, mientras que el área no sobrepasa la del círculo exterior. |
página principal
astronomía | ciencias | ambiente | equidad | tecnología | educación | matemática | salud
nuestra fundación | programas | afiliación | productos | cientec@cientec.or.cr
© Fundación CIENTEC 2001