Fundación CIENTEC

Un cuadrado y sus transformaciones
Alejandra León Castellá, Fundación CIENTEC

Reconocimiento de formas: lo que dice la investigación Origen del Origami El cuento del cuadrado Recomendaciones Bibliografía y Referencias

¡Cuéntenos sus experiencias!

Este artículo pretende documentar un acercamiento multidisciplinario y sensorial a la geométría y su enseñanza en los primeros años (pre y escolares) con el fin de facilitar una aprendizaje más creativo y efectivo.

Presenta enfoques de la investigación del aprendizaje, recomendaciones para profundizar y afianzar el conocimiento y utiliza un cuento como el contexto para explorar una forma y sus transformaciones por medio del Origami, técnica oriental de doblado de papel.

Reconocimiento de formas: lo que dice la investigación
Muchos han estudiado el proceso de reconocimiento de formas geométricas, los efectos de la enseñanza memorística y repetitiva en los primeros niveles y sus consecuencias: la adquisición de conceptos limitados o erróneos y el desinterés de los estudiantes a mediano y largo plazo.

Estas investigaciones afirman que un contenido reducido y la metodología mencionada, con poca manipulación de objetos y procesos matemáticos, no proporcionan las oportunidades necesarias para trascender los prototipos utilizados. Así entonces, el triángulo en preescolar tiene siempre su base sobre la horizontal, es equilátero y hasta puede tener un color determinado: rojo. El cuadrado es azul y el círculo es amarillo. Si las y los estudiantes bajo este sistema son enfrentados con leves modificaciones del triángulo, inclusive rotación del mismo, cabe la posibilidad de que no lo reconozcan..

Según Clements y Sarama, dos investigadores que desarrollan aplicaciones computacionales para la enseñanza y aprendizaje de la geometría y el temprano desarrollo de ideas matemáticas, niñas y niños pasan por varias etapas en su acercamiento a las figuras geométricas. En el primero estadío, el precognitivo, niños y niñas perciben las formas pero son incapaces de distinguirlas y clasificarlas. En la siguiente, la etapa visual, son capaces de identificarlas de acuerdo a su apariencia. Por ejemplo identifican un rectángulo, "… porque se parece a una puerta". No es sino hasta después, en la etapa descriptiva, en la que aprenden a reconocer y caracterizar las formas, basándose en sus propiedades. Es hasta entonces, que habiendo asimilado los conceptos y no solo repitiendo una serie de palabras, que reconocen y describen conscientemente un rectángulo, como una forma que tiene dos lados iguales y cuatro ángulos rectos.

Se puede alcanzar este nivel de pensamiento en los años escolares intermedios, pero algunos no lo logran hasta mucho después y otros nunca lo adquieren. Esto depende mucho del tipo de enseñanza a la que han sido expuestos y sus otras experiencias y aprendizajes obtenidos fuera del aula.

Para impulsar esta evolución, las corrientes pedagógicas de avanzada sugieren técnicas de trabajo complementarias, como las siguientes:

• el acercamiento a los temas desde diferentes disciplinas,

• la manipulación y transformación física y virtual de objetos,

• el establecimiento de conexiones entre el conocimiento previo, los nuevos conceptos y la vida diaria de estudiantes,

• el trabajo en grupos que promueva, el debate de ideas, la clarificación de conceptos, el desarrollo de estrategias individuales y colectivas, y la presentación de resultados ante sus compañeros,

• y la repetida práctica de solución de problemas (en diferentes escenarios), en los que se utilicen destrezas, conceptos o procesos matemáticos.

Marilyn Burns, una líder en pedagogía de la matemática en los Estados Unidos insiste en procesos más extensos de resolución de problemas, que favorezcan también el descubrimiento de patrones, la incorporación de un nuevo léxico en contexto y el desarollo de una mente flexible en el paso del pensamiento concreto al abstracto, de lo específico a lo general.

La meta final de la educación debe ser siempre el impulsar el crecimiento cognitivo en todos — aunque hayan grandes diferencias entre los estudiantes en un mismo aula— y la paulatina autonomía de alumnas y alumnos ante el mundo, un requerimiento básico de la era de la información: ser aprendices continuos.

Esrta propuesta de acercamiento práctico al cuadrado y sus transformaciones, por medio de un cuento y la técnica del origami, permite practicar muchos de los procedimientos recomendados y fortalecer el conocimiento de las formas geométricas básicas. A continuación una introducción al origen del arte.

Origen del Origami
El Origami o papiroflexia, más que un arte japonés, es parte integral de su cultura desde hace más de mil años. Su técnica está basada en el doblado de papel para crear estimulantes y bellas figuras bi y tridimensionales. Inicialmente fue practicado por la Corte Imperial como recreación y pasatiempo y luego se extendió al resto de la población. Más tarde fue llevado a occidente y ahora es fomentado en círculos de aficionados (jóvenes y adultos) en todo el mundo.

El origami clásico utiliza papel cuadrado y no permite cortes en el papel. Pero en su evolución se han creado movimientos con papel rectangular y otros polígonos iniciales.

El papel comercializado para la papiroflexia, es fino y colorido, se parece al papel satinado, pero es más liviano. Para hacer prácticas se puede usar papel bond 16 o buscar papel de regalo satinado y liviano, preferiblemente de un solo color o con diseños muy pequeños.

En algunas modalidades se construye la forma con papel blanco o de color y luego se decora, de acuerdo al objeto, ya sea coloréandolo y pegándole otras formas u objetos. Por ejemplo, un ángel de origami se puede adornar con un librito de canto doblado y un halo de metal.

En tendencias de avanzada de la enseñanza de la matemática, se incorporan las técnicas del origami para enseñar geometría. He aquí un estimulante ejemplo que mezcla el desarrollo de un cuento infantil con la transformación de un cuadrado en diferentes figuras.

El cuento del cuadrado
Traducción libre por Alejandra León Castellá

a) Había una vez un pequeño cuadrado…

b)Estaba muy triste, porque nadie quería jugar con él.

"Ay", lloraba," si yo fuera tan flaco como mi hermano el rectángulo, o tan redondo como el círculo, o si yo tuviera esquinas tan preciosas como mi hermana el triángulo… Pero yo no tengo nada especial, todas mis esquinas son igual de largas y aburridas."

Entonces tomó un… libro muy interesante y leyó este cuento.

c) Había una vez una pequeña bruja que dormía todo el día y volaba toda la noche en su escoba por el cielo ennegrecido. Hacía tanto frío, que siempre le daba por estornudar, hasta que se enfermó.

Entonces se buscó un… pañuelo y se limpió la nariz.

d) Su madre al verla estornudar le dijo: No podés salir más de noche a volar en tu escoba. Mejor trae tu… velero. Y haz un pequeño viaje. El aire del mar te va a sentar bien.

e) Obediente, la brujita, tomó su velero y viajó por todos los mares hasta que descubrió en una bellísima play una… casa de brujas.

f) "Aquí quiero quedarme", pensó la pequeña bruja y le escribió a su madre una… carta.

g) " Mami, debés venir a visitarme. Mi casa de bruja es tan linda y tengo una excelente vista desde mi… ventana."

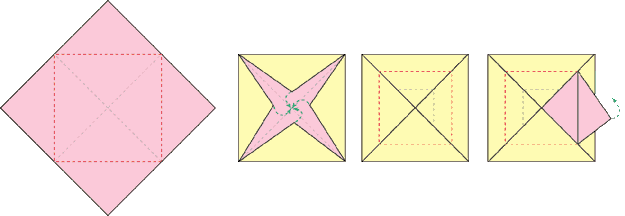
h) Al leer la carta, la mamá se fue hacia su… armario.

i) Allí se buscó un bellísimo… pañuelo de lunares rojos.

i) "Este es exactamente el correcto", pensó ella. "El pañuelo me mantendrá el pelo acomodado." Ella se lo probó frente a su… espejo viejo.

k) La bruya estaba ambienta, entonces antes de tomar su escoba, para ir a visitar a la pequeña bruja, decidió freirse un riquísimo… pescado.

l) Y de postre buscó una tableta de… chocolate.

m) Después alistó su… cartera grande.

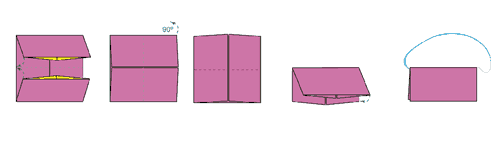
n) Y se montó en su escoba. "Oh, se me olvidaba algo.", dijo, mientras regresaba a su casa a buscar una… bolsa mágica.

0) Así se montó en su escoba y viajó por encima de los mares del mundo, hasta que finalmente encontró a la pequeña bruja que jugaba en la playa mientras observaba una colorida… mariposa.

p) "Que es esa horrible criatura", dijo la madre. Sacó una varita mágica y transformó a la mariposa en un gordo y horrible… sapo.

q) "Por favor no lo hagas", dijo la pequeña brujita. A mi me gustaba la bella mariposa. "Pues a mi me gusta más el sapo", dijo la madre. Pero por suerte pasó por allí otra mariposa y las dos se sintieron felices. Y desde entonces vivieron felices hasta su muerte.

Nuestro pequeño cuadrado cerró el libro y se frotó los ojos. ¿Estaba despierto o soñaba? ¿ Será posible que todas estas cosas se puedan hacer al doblar un simple cuadrado? Entonces, eso quiere decir que todas estas formas están dentro de mi: un libro, un pañuelo, un bote, una casa, la carta, la ventana, el armario, el pañuelo para la cabeza, el espejo, el pez, el chocolate, la bolsa mágica, la mariposa y el sapo.

"Ahora creo que si podré encontrar niños y niñas que quieran doblar todas esas formas conmigo. Ahora no voy a aburrirme." Y, de pura alegría y entusiasmo, el cuadrado se tornó… rojo y brillante.

RECOMENDACIONES
Es importante hacer algunas advertencias sobre esta propuesta y su realización con las y los más pequeños. El origami es un arte que requiere de paciencia, orden y secuencia en el aprendizaje. El tamaño del cuadrado para manitas pequeñas no debe ser ni muy grande ni muy pequeño, entre 16 a18 centímetros de base es apropiado para empezar. Se puede practicar con papel blanco primero y luego pasar a papeles de colores. Para reafirmar el autoestima y fortalecer la memoria, es importante practicar muchas veces una misma figura. Luego usarla, en la medida de lo posible, como la base para la próxima figura. El cuento así lo sugiere. Se parte de un cuadrado que se dobla solo una vez (b) por la mitad para formar un libro. Este libro (c) es la base del próximo, que requiere solo otro doblez, por la mitad más corta, para convertirse en un pañuelo y así sucesivamente: El libro es la base del armario (h), el armario es la base de la barra de chocolate (l), la barra de chocolate es la base de la cartera (m), etc.

Además, muchas de estas figuras no trascienden el papel hasta que no se decoran con algunos elementos (dibujados o pegados): los lunares del pañuelo, los contenidos del libro y las perillas del armario, la puerta y las ventanas de la casa, etc.

CONCLUSION
La práctica continua con papel puede permitir que docentes, madres y padres de familia y estudiantes visualicen las formas geométricas, las relacionen con lo que conocen a su alrededor, practiquen el orden en un proceso, realicen secuencias de pasos y manipulen las formas (dimensiones, proporciones, simetrías, rotación, etc.), mientras practican y perfeccionan destrezas motoras finas, crecen en abstracción y creatividad y descubren y se apropian de las figuras en sí. Porque, como decía Frank Openheimer, solo las cosas que descubrimos nosotros mismos, son realmente nuestras, aunque otras personas las hayan descubierto antes.

Bibliografía y Referencias

1 Clements,Douglas & |Sarama Julie, Young Children´s Ideas about Geometric Shapes, Revista Teaching Children Mathematics, Volume 6, Number 8, April 2000, National Council of Teachers of Mathematics (ISSN 1073-5836)
2 León Castellá, Alejandra, Aprendizaje Cooperativo, Fundación CIENTEC, San José, Costa Rica,1999.
3 Burns, Marilyn, About Teaching Mathematics, Math Solutions Publications, enero 1999, USA, ISBN0-941355-05-5
4 Aytüre-Sheele Zülal, ORIGAMI, Hamlyn Creative Crafts, Octopus Publishing Group, London. 1989
5 Kindergarten, Colegio Humboldt, Die Geschichte vom Quadrat. San José, Costa Rica 1997.
6 Frank Openheimer, fundador del museo de percepción, ciencia y arte The Exploratorium, San Francisco California.

---

Esta ponencia, tipo taller participativo, fue presentado en el II Festival de Matemática, realizado en la Universidad Nacional, Heredia, Costa Rica, en mayo del 2000.

Otras en Memorias del II Festival de Matemática